Matematik – Taksonomiske niveauer

Matematik adskiller sig fra flere andre fag, ved at vi sjældent eller aldrig kommer over det ”redegørende” niveau, som til gengæld kan underinddeles efter graden af forståelse af emnet.

Af denne grund anvender vi SOLO-taksonomi. Det er en taksonomi, der bygger på, at viden består af elementer. Jo flere af disse elementer, man kan sætte sammen på en korrekt måde, desto højere niveau er man på. Det kan illustreres på følgende måde:

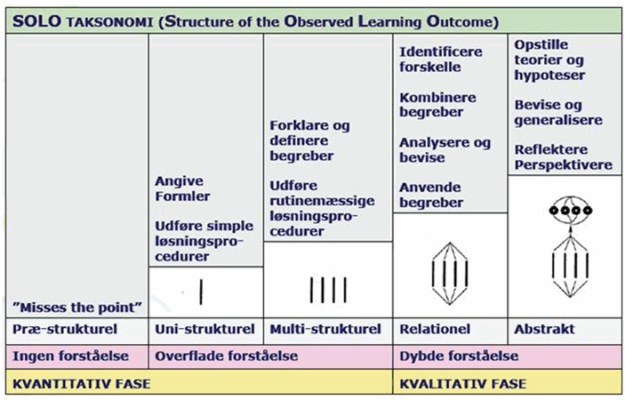
Illustrationen kan oversættes til følgende korte fortolkning:

1. Det ikke-strukturelle niveau. Her kender eleven mange fakta, men kan ikke binde dem sammen i en struktur
2. Det enkelt-strukturelle niveau. Eleven forstår indlysende og logiske sammenhænge, men har ingen dybere forståelse herfor
3. Det fler-strukturelle niveau. Eleven ser mange sammenhænge, men kan ikke se den overordnede sammenhæng
4. Det relationelle niveau. Eleven ser sammenhænge mellem de enkelte dele og den overordnede sammenhæng
5. Det udvidet abstrakte niveau. Eleven kan generalisere, perspektivere og bruge sin viden i andre sammenhænge

Et eksempel fra matematik:

De fleste elever kan nikke genkendende til, at de kender Pythagoras’ læresætning. Der findes i midlertidig mange forskellige måder på, hvor godt man forstår læresætningen. Jo højere man kommer op gennem trinene desto flere videnselementer skal man kende.

Trin 1: Eleven kender Pythagoras’ læresætning: a² + b² = c²

Trin 2: Eleven ved, at den kun gælder i retvinklede trekanter, og kan beregne siden c, hvis de to øvrige sider kendes.

Trin 3: Eleven bruger generelle begreber som kateter og hypotenuse. Eleven er i stand til at finde en vilkårlig af siderne og kan anvende Pythagoras i mere komplicerede opgaver med fx en ligebenet trekant.

Trin 4: Eleven kan gennemføre et bevis for Pythagoras’ læresætning.

Trin 5: Eleven kan anvende Pythagoras’ læresætning i forbindelse andre matematiske emner og beviser.