Videnskabsteori – Matematiske metoder
Matematikken er opstået som en metode til at behandle tal (aritmetikken) og figurer (geometrien) og har udviklet sig til en videnskab om abstrakte strukturer. Udviklingen er dels drevet af selve ønsket om abstraktion og generalisering, dels af forsøg på at løse forskellige problemer både af ren matematisk natur og problemer, der er opstået ved matematiske beskrivelser af naturen eller menneskeskabte fænomener. Derved er der opstået nye matematiske begreber og discipliner.
Den grundlæggende arbejdsmetode indenfor matematik er den aksiomatisk-deduktive metode, som blev udviklet i det klassiske Grækenland (ca. 500 f.Kr), hvor matematikerne begyndte at insistere på, at matematiske resultater skulle kunne bevises (deduceres) ud fra eksplicit formulerede forudsætninger (aksiomer).
Aksiomatisk-deduktiv metode
Den aksiomatisk – deduktive opbygning mødes første gang i 13 binds værket ”Elementerne”, som blev skrevet af matematikeren Euklid ca. 300 f. Kr. Selvom det har en del skønhedsfejl, er opbygningen et særkende ved al moderne matematik. Den deduktive opbygning af matematik består af begreber og definitioner, aksiomer og sætninger med beviser, og den logisk deduktive arbejdsmetode kan i hovedtræk beskrives som følger:
- Som udgangspunkt starter man med nogle grundlæggende begreber, som bruges i definitionerne. Hos Euklid bruges begreberne punkter og linjer til at definere ex.vis trekant.
- Herefter opstiller man nogle simple og oplagt sande påstande (aksiomer[1]) baseret på begreberne og definitionerne. Antallet af aksiomer skal holdes på et absolut minimum. Euklid opstillede således kun 5 aksiomer for hele geometrien, hvoraf et var ”To punkter fastlægger en linje”.
- Man kombinerer nu aksiomer, definitioner og begreber ved brug af logik og udleder sande påstande. Disse påstande kaldes sætninger, og udledningen dvs. argumentationen, der fører frem til sætningen, kaldes et bevis.
Når først man har bevist en sætning, kan man bruge sætningen sammen med andre beviste sætninger, begreber, aksiomer og definitioner til at bevise endnu flere sætninger.
Den aksiomatisk-deduktive arbejdsmetode kan stærkt simplificeret illustreres på følgende måde:
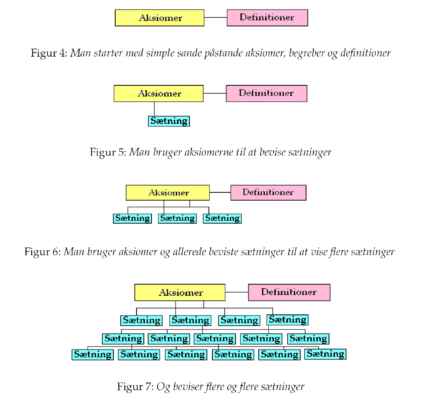
Figur 1: Skematisk fremstilling af aksiomatisk deduktiv arbejdsmetode
(Kilde: Naturvidenskab og Matematik – lidt om metoder til AT, Virum 2009)
Matematisk modellering
Matematisk modellering blev en disciplin indenfor anvendt matematik i 1960’erne ved fremkomsten af computerne og vinder fortsat frem på flere og flere af de områder, hvor man bruger matematik som f.eks. naturvidenskab, teknik, økonomi, samfundsfag m.m.. En af grundene til denne udvikling er den enorme regnekapacitet og regnehastighed, som vi har fået. Computere gør os i stand til at finde numeriske løsninger[2] til store matematisk komplicerede modeller. Før computerne var man henvist til at modellere med systemer med analytiske løsninger3 eller give sig i kast med ekstremt tidskrævende numeriske metoder.
Ordet model stammer fra det latinske ord modulus, som betyder mål og forstås i betydningen forbillede eller mønster. Det som modellen afbilleder kaldes det virkelige system. Som eksempler på tidlige matematiske modeller kan nævnes modeller for vores solsystem. I middelalderen forestillede man sig Jorden som fast og ubevægelig, mens solen og planeterne bevægede sig rundt på forskellige sfærer (Ptolemæus verdensbillede). I slutningen af middelalderen fremkom Kopernikus med en anden model, der placerede solen som centrum for de øvrige planeters cirkulære bevægelser.
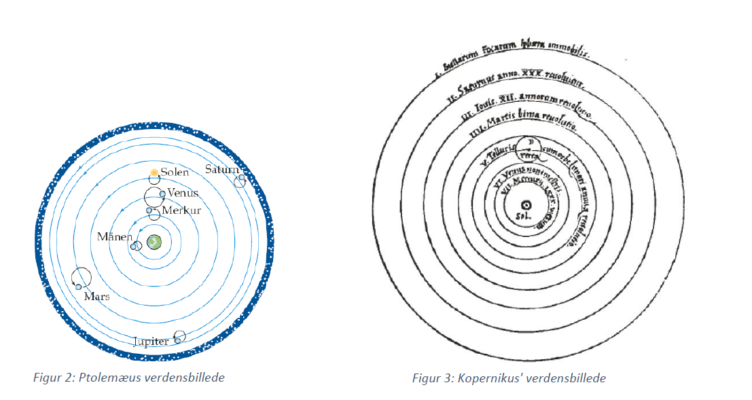
Set med modeløjne, var Kopernikus’s model ikke ”bedre” en den gamle model, da den ikke var bedre til at forklare de astronomiske data, man havde indsamlet. Først med Keplers beskrivelse af planetbevægelser observeret af Tycho Brahe med ellipser i stedet for cirkler, blev Kopernikus model almindeligt accepteret.
Den grundlæggende modellering
Begrebet matematisk model skyldes filosoffen og matematikeren Rene Descartes (1596–1650). Descartes introducerede og udviklede begrebet matematisk model ud fra en vision om, at han kunne finde en universel matematisk metode til at beskrive ethvert tænkeligt problem fra virkeligheden og angive en løsning til problemet. Ifølge Descartes kan problemløsning opdeles i trinnene
- Reducer problemet til et matematisk problem
- Formuler det matematiske problem som et algebraisk problem[3]
- Reducer det algebraiske problem til løsning af en ligning
Selv om Descartes drøm om en universel model aldrig blev realiseret, findes der mange problemstillinger fra virkeligheden, som kan løses i denne ”ånd”.
George Pólya (1887-1985) var en matematiker, som ved siden af matematik også beskæftigede sig med strategier til løsning af problemer. Hans mest kendte bog herom fra 1945 har den meget sigende titel ”How to solve it?”. Han angiver ikke en universel metode, men angiver sine overvejelser/tankerne til en strategi ved løsning af problemer og modellering. Polya opererer med fire trin ved problemløsning
- Forstå først problemet. For at gøre sig klart, hvad der er problemet, skal man gøre sig klart hvad er ukendt, Hvad er kendt, hvad er forudsat. Dernæst skal man overveje om forudsætningerne kan være opfyldt, om man har oplysninger nok til at bestemme det ukendte, om oplysningerne er modsigelsesfri. Man skal analysere forudsætningernes forskellige dele, formulere dem og skrive dem ned.
- Find en matematik løsningsmetode. For at gøre det må man overveje følgende. Har jeg set problemet eller et tilsvarende tidligere? Kender jeg en nogle resultater jeg kan bruge? Man ser altså på det ukendte, og forsøger at relatere det til problemstillinger, der omhandler samme ukendte størrelser, men hvis løsninger man allerede kender. Hvis man ikke kan løse problemet, kan man først forsøge at løse nogle beslægtede problemer ved at ændre lidt på forudsætningerne eller det ukendte. Efterfølgende må man så tjekke, at man har fået brug for alle forudsætningerne og alle oplysningerne.
- Udfør beregningerne. Kontroller hvert trin i beregningerne. Man skal kunne vise at hvert trin er korrekt.
- Undersøg løsningen. Dette gør man ved at prøve at kontrollere resultatet og evt. få den samme løsning på en anden måde. Man skal overveje, om man kan anvende resultatet og/eller metoden på et andet problem.
Polyas tanker genfindes i nutidig matematisk modellering, hvor man deler modelleringsprocessen Op efter følgende mønster
i) Forstå problemet og afgræns det.
ii) Vælg løsningsmetode: matematisk metode/algoritme/program, som kan give en løsning.
iii) Gennemfør beregningerne evt. med forskellige parametre.
iv) Undersøg egenskaberne ved løsningen.
v) Juster modellen. Forbedr om muligt modellen.
Skematisk kan modelleringsprocessen simplificeret opskrives således:
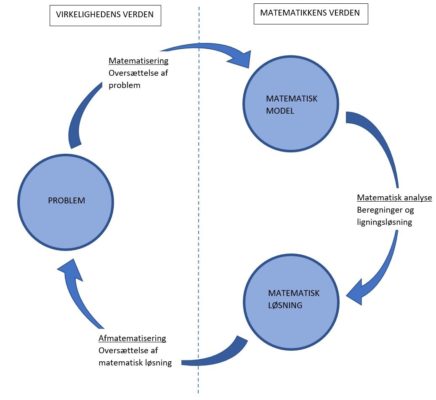
Figur 4: Skematisk fremstilling af modelleringsproces (Kilde: MKP Allerød Gymnasium)
[1] Aksiomer er ”født” sande. Der findes flere tilfælde i matematik, hvor man har måtte justere aksiomerne.
[2] Numerisk løsning er en tilnærmet (talmæssig) løsning til en ligning. Numeriske metoder giver ALDRIG mere end EN mulig (tilnærmet) løsning på problemet, og vælges derfor kun, hvis det ikke er muligt at løse problemet analytisk. 3 En analytisk løsning er en eksakt fuldstændig løsning til en ligning, der beskrives med tal eller bogstaver.
[3] Algebra er bogstavregning og læren om matematiske operationer med disse.